EL TOPOGRAPHO

Este artículo trata el uso de la topografía en las misiones de prospección arqueológica llevadas a cabo en la necrópolis bizantina de Tall as-Sin, provincia de Deir ez-Zor (Siria). Cuando se representa la superficie de la tierra correspondiente a un yacimiento arqueológico, el objetivo que se persigue es cartografiar la zona de estudio de manera precisa, de forma que todos los afloramientos naturales y/o artificiales aparezcan representados en su lugar y con una simbología adecuada, fácilmente entendible. Asimismo, la cartografía de detalle en arqueología es de suma importancia ya que puede aportar datos relevantes en cuanto a dimensiones, las orientaciones de los elementos, sus estructuras y su origen. Por esta razón es fundamental representar los elementos característicos del paisaje como son sus vaguadas, las carreteras, las curvas de nivel, entre otros que junto con la arquitectura que se halle en la zona, aporta un significado esencial para entender y estudiar, la prospección y la excavación.

1. INTRODUCCIÓN

Este artículo se centra en el estudio topográfico detallado de Tall as-Sin, situado a los pies del antiguo cauce del río Éufrates, en la provincia de Deir ez-Zor, Siria . En esta zona se aprecian múltiples asentamientos de distintas civilizaciones antiguas.

El eje del Éufrates siempre ha sido desde la antigüedad un canal por medio del cual los pueblos intercambiaban mercancías debido a que es en su gran mayoría navegable. Esta zona requiere un estudio arqueológico de gran extensión, que permita reconstruir con certeza el pasado. Para ello se requiere la integración de datos de diferentes disciplinas, siendo la Topografía una de ellas

El trabajo topográfico se integra en una prospección que documenta un asentamiento Bizantino del s. VI d.c., que consta de una muralla y de unos enterramientos en las afueras de la ciudadela (necrópolis). El presente artículo muestra el proceso cartográfico seguido para documentar esta zona con el fin de contribuir a su estudio cartográfico y su actualización.

2. LUGAR DE TRABAJO

La Fig. muestra una fotografía del entorno de actuación, con Tall as-Sin (“Colina del diente”) al fondo. La parte superior de dicha figura muestra la colina, donde supuestamente existió una torre y una acrópolis; la parte más baja, el antiguo cauce del río Éufrates. Vista panorámica de Tall as-Sin. La zona de mayor elevación se corresponde con la muralla o el recinto del asentamiento Bizantino.
En principio no se disponía de información topográfica de partida a escalas grandes o medias. Solo se contaba con la existencia de mapas a pequeña escala que permitían situarnos en el terreno pero no localizar detalles, o entidades con suficiente grado de resolución y precisión.



3. FASES DE TRABAJO DE CAMPO Y GABINETE

3.1. Observación en campo

Se procedió, en primera instancia, a un estudio previo de la zona de Tall as-Sin en campo y en gabinete, se definieron las bases o vértices que van a definir la red topográfica de este levantamiento.

La extensión de la zona de actuación, 133 hectáreas, la homogénea tonalidad de la tierra, la calima del lugar y el factor viento, propició la marcación de las estaciones de la red topográfica con banderolas de color fácilmente visibles a distancia

El material que se utilizó primeramente en campo fue:

• Barras de hierro. Martillo.
• Banderas de color rojo.
• Prismáticos.
• Estación total

La planificación y observación de los vértices de la red fue la siguiente: Reparto de la zona por grupos de observadores y análisis de la red por zonas a fin de evitar el máximo de estacionamiento múltiple en algún vértice. Para ello se definieron estaciones temporales que, una vez comprobada su visibilidad global, se fijaron como estaciones permanentes. Mientras un grupo de observadores se colocaba en un vértice, el siguiente grupo, con la ayuda de los palos y las banderas, iba estudiando la zona, y procedía a la instalación de bases temporales.
Personal clavando la estación temporal. Base establecidad de forma permanente con ayuda de banderas y círculos en el suelo. Una vez situada la base temporal (susceptible de ser permanente), otro grupo de observadores colocados en diferentes puntos estratégicos divisaba, gracias a las banderas instaladas, si efectivamente ese punto era visible entre sí. En caso afirmativo, el punto pasaba a ser considerado como permanente .




Posteriormente, se realizó la observación de la red desde cada uno de los vértices permanentes .
3.2. Comprobación de la constante del prisma




En este estudio, la temperatura media obtenida en las horas de trabajo fue aproximadamente de +35ºC, y una presión atmosférica de unos 1013 milibares, que transformados a mm Hg equivalen a 759,81mmHg.

A continuación se muestra la fórmula de la corrección atmostérica1 (en m):





Ka : Valor de la corrección atmosférica.
P : Presión atmosférica ambiental (mmHg).
t : Temperarura atmosférica (ºC).
La distancia L(m), después de realizar la corrección atmosférica, se obtiene a partir de:
L = l (1+Ka)

Siendo l: Distancia medida sin realizar la corrección atmosférica. A modo de ejemplo, comprobamos que para una distancia de 1000 m, se obtiene un factor de corrección de 1.8 cm.




1. Topcon. Manual de usuario de la Estación total GTS-220, 2003.

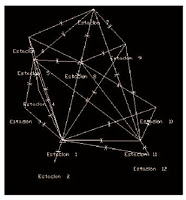
La geometría de la red se diseñó de manera que fuera lo más regular posible, pues el buen diseño de la red a priori permite obtener buenos resultados a posteriori.


CORRECCIONES VARIABLES

-0.010 X (3) 613306.010
-0.021 Y (3) 3909205.679
0.006 X (4) 613386.576
-0.007 Y (4) 3909307.853
0.013 X (5) 613354.283
-0.044 Y (5) 3909485.956
0.016 X (6) 613325.716
-0.061 Y (6) 3909614.329
0.003 X (7) 613704.393
0.006 Y (7) 3909778.676
0.004 X (9) 613894.029
-0.003 Y (9) 3909575.257
-0.010 X (10) 614069.530
-0.004 Y (10) 3909207.996
-0.019 X (11) 613978.449
0.003 Y (11) 3909016.563
-0.014 X (12) 614029.796
0.001 Y (12) 3908933.140

El proceso de cálculo y compensación de una red, no incluye únicamente la determinación de las variables coordenadas, sino que estas deben ir acompañadas del correspondiente estudio estadístico de los resultados obtenidos.
Por este motivo el modelo matemático utilizado, incorpora un modelo estadístico-estocástico modelo Gauss-Markov2.
En este modelo matemático y estadístico, la hipótesis de partida consiste en que los observables siguen una distribuciónnormal, además se considera que el estimador de la desviación típica del observable de peso unidad a priori es igual a uno. Por lo tanto, el estimador de la desviación típica del observable de peso unidad a posteriori, debe aproximarse en la medida de lo posible a este valor estimado.

El resultado obtenido en la compensación de la red ligada es:

Número de grados de libertad, n = 28

Estimador de la varianza observable de peso unidad = 0.793

Estimador desviación típica de peso unidad = 0.890

Estos estimadores estadísticos nos definen la calidad del trabajo realizado. Como se aprecia los grados de libertad son 28, este dato nos muestra el número de redundancias que se tienen en las observaciones. Por otro lado, el estimador de la varianza de peso unidad nos ofrece información sobre la validez de la precisión supuesta de partida. Un valor a posteriori próximo a uno indica, que la suposición inicial se cumple, lo que implica, que los errores estimados a priori son acordes a la observación realizada. Los resultados fueron aceptables, teniendo en cuenta todos los condicionantes atmosféricos sometidos en el momento de la observación.Una vez se procedió al cálculo y compensación de la red, se obtuvieron las coordenadas compensadas y ajustadas de los 12 vértices que componen la red. De este modo, estuvimos en disposición de proceder al levantamiento topográfico de la zona.

3.6. Conversión de la altitud elipsoidal a altitud ortométrica

Para pasar de coordenadas altimétricas elipsoidales a ortométricas se empleó el modelo global de geoide EGM96, debido a que no se disponía de ninguna referencia altimétrica de partida. Con este modelo se pudo hallar la altitud ortométrica, ya que a partir de EGM96 se puede determinar la ondulación del geoide, N. La altura ortométrica, H, se obtiene restando la altura elipsoidal h (dada por el GPS) según:
H = h - N
2. Chueca, Berne, Herráez, 1996.

De esta forma, todas las altitudes fueron referidas a un sistema altimétrico absoluto global. Tanto los datos planimétricos como altimétricos estaban adaptados a un sistema de referencia absoluto materializado por bases.

4. PRODUCTOS DERIVADOS

4.1. Planos y perfiles Topográficos
El Mapa Topográfico de Tall as-Sin se realizó a escala 1:1000, con una equidistancia entre curvas de nivel de 1 m En este tipo de misiones arqueológicas es muy importante que la equidistancia entre las curvas de nivel sea pequeña, ya que a partir de ellas se obtiene información de detalle muy importante en estudios arqueológicos. Permite determinar por ejemplo el desnivel entre la muralla y la ciudad, la pendiente de la misma, la altura de las torres, la extensión de la prospección, el emplazamiento y disposición de las tumbas. Además, se le asociaron datos adicionales como son las principales carreteras (Fig. 10), las instituciones públicas o los elementos artificiales característicos del terreno que resultaron fundamentales a la hora de conocer el contorno de la ciudad y explicar su asentamiento.
Una de las informaciones más importantes en el estudio arqueológico fue el contorno de la muralla. A partir de él, se situaron las entradas principales a la ciudad, la dimensión exacta de la ciudadela, y la estructura de dicha ciudad (permitiendo hacerse una idea de la morfología urbana).

El levantamiento topográfico también contempló el posicionamiento minucioso de las tumbas bizantinas que estaban enterradas en el área  y que formaban parte de una antigua necrópolis.

Se les dotó de coordenadas absolutas a las entradas de todas las tumbas bizantinas , sumando un total de 168, todas ellas subterráneas, y referidas a un sistema de referencia absoluto que permitió estudiar su orientación (p. ej. al Sol, hacia el Este, o alguna otra dirección a destacar). Estos datos se estiman muy importantes cuando se estudian las tumbas de cualquier asentamiento.

También se generó un perfil longitudinal de la zona, que nos define la pendiente que existe en la ciudadela, entre la colina, la muralla y el río.

El perfil longitudinal va desde el punto más alto de esta ciudadela, que se correspondería con una torre, hasta uno de los puntos de la muralla, que coincide exactamente con el inicio de uno de los sondeos arqueológicos. Se aprecia como existe una gran diferencia de altitud en la parte derecha, que es la zona por donde pasaba el río Éufrates. Por otro lado, se observa una ligera elevación, al final del perfil longitudinal, que coincide con la muralla de la ciudadela.



En otro orden de ideas, también se realizó un control exhaustivo de los sondeos arqueológicos, ya que era de vital importancia que todos los restos encontrados se situaran en niveles (profundidades) diferenciadas del terreno, junto con su cota y situación planimétrica. Se les dotó de coordenadas absolutas cada vez que se excavaba un nivel diferente, o cuando aparecía un nuevo elemento en los sondeos. A continuación se muestra uno de los planos topográficos de la zona a escala 1:500 .

4.2. Creación de un Modelo Digital de Elevaciones (MDE)

Un modelo digital del terreno (MDT), representa la distribución espacial de una variable cuantitativa y continua. Cuando esta variable es la cota del terreno, se denomina Modelo Digital de Elevaciones (MDE).

Los MDE facilitan la realización de estudios topográficos de la zona, así como extraer e interpretar pendientes u otras formas artificiales del terreno que ayudaran a delimitar la ciudadela.

La información altimétrica de origen se consiguió mediante el levantamiento topográfico que se realizó en la zona. Se observaron un total de más de 4.000 puntos topográficos .

Para poder realizar el modelo de la superficie es necesario acudir a métodos de interpolación, ya que no es posible medir todos los puntos de la superficie. Estos métodos de interpolación espacial permiten calcular el valor altimétrico de toda la superficie conociendo el valor de esa variable en otras posiciones. Los interpoladores utilizados aquí (locales), operan sólo dentro de una pequeña zona alrededor del punto a interpolar, de tal forma que un cambio en un dato muestral solo afecta a una pequeña zona.

Existen varios métodos de interpolación, y dependiendo de la precisión requerida, de los datos de partida, de la orografía del terreno, y demás factores, será más representativo uno u otro.

En principio, se utilizó el método de interpolación Krigeado para representar los gráficos tridimensionales (Fig. 16). El Krigeado es un método geoestadístico (estadística relacionada con los datos geográficos3), que ofrece una gran flexibilidad, considerando tanto las distancias como la geometría de la localización de muestras.

La cota interpolada se obtiene por cálculo de la media ponderada de un número predeterminado de puntos muestrales. La salida que se obtiene con este tipo de interpolación es una imagen raster. Su estructura es tipo grid y está formada por celdillas de igual forma y tamaño, que hacen referencia a una determinada zona de la superficie terrestre. Los valores numéricos se asignan a los centros de las celdillas, lo que implica que la precisión variará con la resolución de la celdilla. Por tanto, los datos originales no son respetados excepto si éstos coinciden con el centro de celdilla. La estructura raster presenta como positivo la fácil y rápida gestión de la información.

Una de las ventajas que cabe destacar del Krigeado es la capacidad de cifrar el error en el valor del modelo digital. Por tanto, toda cota resultado del proceso de interpolación viene acompañada por una estimación acerca de la varianza de la superficie4.
El modelo raster no permite el tratamiento de discontinuidades topográficas que supongan cambios superficiales bruscos, como fuertes rupturas de pendiente, ya que genera modelos muy suavizados. Debido a esta particularidad, se calculó un modelo digital basado en un TIN (‘Irregular Triangulated Network’).

El TIN se define como un conjunto de triángulos irregulares adyacentes y no superpuestos. Se construye ajustando un plano a tres puntos no colineales. La interpolación que se utiliza es también local, y exacta porque asigna a cada punto el valor resultante de interpolar un plano por los tres puntos muestrales más cercanos. Es el único método que respeta la altimetría original de la zona, a diferencia del modelo raster anteriormente comentado.

Si los puntos definen bien el terreno, el TIN ,podrá representar de forma precisa una superficie con menos puntos que otros modelos. Se utiliza el algoritmo de Delaunay, es el método más habitual de triangulación, debido a que sus triángulos intentan ser lo más equiláteros posibles. Es más rápido que un raster, pero ocupa más memoria. Es el más satisfactorio para superficies topográficas con fuertes discontinuidades, porque se adapta a la complejidad del terreno, conformando una red de triángulos más densa allí donde es mayor el número de puntos muestrales.

Visualmente, estos modelos ofrecen un grandísimo potencial, pues de un simple vistazo a vista de pájaro, posibilita la interpretación orográfica del terreno, resaltando sus características más importantes, como la muralla o la torre de la ciudad y el antiguo cauce del río, que es la zona más baja y totalmente plana.

Tras obtener el TIN se procede a superponer la cartografía de la zona, obtenida por métodos topográficos, sobre dicho modelo digital. Se obtiene una visión 3D muy acertada del terreno, y esto permite establecer diferentes análisis y estudios sobre el asentamiento Bizantino de una forma más precisa, ya que permite estudiar la posición planimétrica de la muralla, la acrópolis y necrópolis del asentamiento junto con la orografía del terreno, gracias al Modelo 3D.

Por último, se crea un video de un vuelo tridimensional , realizado sobre el modelo digital con la cartografía de la zona de estudio superpuesta. Se procede al tratamiento, edición y maquetación de dicho video para que pueda ser visualizado vía WEB por cualquier usuario.

5. CONCLUSIONES

En misiones arqueológicas, la topografía y las técnicas cartográficas posibilitan la generación de productos que ayudan sobremanera a posicionar en el terreno, de forma inequívoca, las diversas manifestaciones humanas y geográficas en documentos tales como los planos o mapas topográficos y/o temáticos. Los mapas topográficos, los perfiles y los MDE son útiles a la hora de hacer estudios sobre las pendientes o estructuras de la ciudad. El estudio de las vaguadas, de las estructuras montañosas, de los factores geográficos, en combinación con la acción antrópica, permite dar explicación a estos asentamientos, satisfaciendo de esta manera estudios orográficos y estudios de prospección arqueológica.

BIBLIOGRAFÍA.
1. TOPCON, Manual Estación total GTS-220, 2003.
2. Chueca Pazos, Manuel, Berne, J.L., Herráez, J, Redes Topográficas y Locales. Microgeodesia. Paraninfo. Madrid 1996.
3. Moral, F.J., Aplicación de la geoestadística en las ciencias ambientales. Ecosistemas XIII/1, 2004.
4. Márquez Pérez, J., Modelos digitales de elevaciones, métodos de interpolación y parámetros morfométricos del relieve. Vol. I. Tesis doctoral, Universidad de Sevilla, 2004.